Les coefficients de couplage
Dans cette page sera abordé le formalisme qui permet de définir précisément les coefficients de couplage, nous commencerons par évoquer le cas le plus connu du couplage par champ magnétique quasi statique qui conduit à une analyse classique qui s'intègre bien dans le cadre des circuits, puis nous détaillerons le cas plus délicat du couplage électrique. Finalement nous montrerons que le condensateur courant correspond au cas très particulier du couplage total mais qu'il existe comme dans le cas magnétique des situations de couplage partiel entre dipôles dont l'utilisation pour le transfert de l'énergie, envisagée par Tesla il y a plus d'un siècle, est introduite ici dans sa généralité.
Le couplage magnétique ou induction
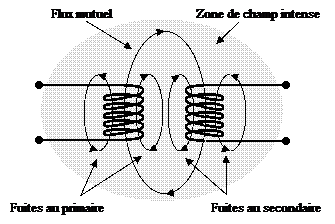
Lorsque deux bobines à induction sont suffisamment proches, le flux magnétique généré par l'une des bobines peut traverser en partie l'autre, lorsque ce flux est variable cela induit une force électromotrice dans cette deuxième bobine. On conçoit aisément que le couplage total sera obtenu lorsque la totalité du flux sera entièrement partagé par les deux bobines. Lorsque ce n'est pas le cas on pourra définir pour chaque bobine un flux de fuite et un flux total qui traverse la bobine considérée, somme du flux mutuel et du flux de fuite.

Circuits magnétiques couplés, flux commun et flux de fuites
Une formulation linéaire
La linéarité de la formule d'Ampère entre champ magnétique et courant local (densité de courant) impose que le champ magnétique en tout point puisse, quelle que soit la configuration pratique, être exprimé par une combinaison linéaires des courants circulants dans les circuits concernés. Cette situation de linéarité peut être étendue aux flux qui traversent chacune des bobines.
![]()
D'après le théorème de réciprocité nous avons L12 = L21 = LM (ou simplement M), on peut aussi poser L11 = L1 et L22 = L2
Nous avons e1 = dɸ1/dt = ɸ1'= L1i1'+LMi2' et e2 = dɸ2/dt = ɸ2'= LMi1'+L2i2' on obtient finalement :
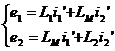 |
Soit sous forme matricielle compacte : |
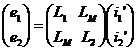 |
Le déterminant du système est : Det = L1L2 - LM², il ne s'annule jamais si : LM² < L1L2
Le coefficient de couplage magnétique se définit simplement par :
![]()
Il apparaît comme le rapport de l'inductance mutuelle à la moyenne géométrique des self inductances. Comme le flux mutuel ne peux pas être plus grand que le flux qui traverse chacun des circuits, le coefficient de couplage est nécessairement plus petit que l'unité, le problème n'est jamais dégénéré.
Les représentations
La représentation la plus généralement utilisée est la suivante :
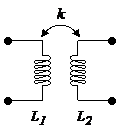
La représentation la plus classique pour le couplage magnétique
Si l'on veut faire apparaître une branche commune ou maille commune, la représentation qui donne les correspondances les plus simples est la représentation en "T":
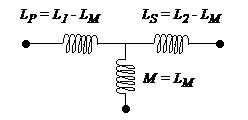
Le schéma équivalent en "T"
Cette représentation ne fait toutefois plus apparaître l'isolement "galvanique" entre les deux portions de circuit. De plus dans le cas où les nombres de tours utilisés dans les deux bobinages sont différents et le couplage assez fort (cas classique des applications de type transformateurs) l'inductance mutuelle peut se révéler plus grande que l'une des self inductances ce qui conduit a une inductance équivalente négative. La représentation précédente reste toutefois valable pour les couplages faibles. Pour éviter le problème de coefficients négatifs dans le cas des couplages forts et des enroulements asymétriques, on est conduit à rajouter dans le schéma un transformateur idéal dont le rapport r est égal au nombre de tours :
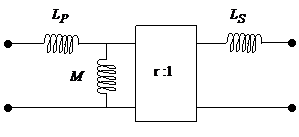
Le schéma équivalent avec des coefficients toujours positifs
Les inductances deviennent alors des effets parasites dont on cherche souvent à minimiser l'importance. Les inductances Lp et Ls représentent les flux de fuites au primaire et au secondaire elles sont appelées inductance de fuites et doivent être les plus petites possibles alors que l'inductance M appelée dans ce cadre inductance de magnétisation doit être la plus grande possible. Notons pour terminer ce petit tour rapide des inductances couplées que dans le schéma précédent on dispose maintenant de quatre paramètres pour décrire une situation qui en comporte seulement trois d'indépendants, on peut donc imposer une contrainte supplémentaire arbitraire mais réaliste entre les quatre paramètres. Par exemple on peut poser Lp = 0 et ramener les fuites au secondaire ou l'inverse.
Le couplage électrique ou influence
L'Influence ou l'Induction électrique
Historiquement on appelait en France le fait qu'un champ
électrique intense fasse apparaître des charges "induites" à distance sur des
matériaux diélectriques ou conducteurs : "électrisation par influence électrique".
Les machines utilisant ce type d'effet furent donc appelées "machines à
influence". Le terme fut utilisé un temps par les anglais mais l'expression
dominante est maintenant "electric induction", ce qui
rajoute une confusion potentielle supplémentaire chez eux.
Le monopole isolé
Nous avons vu précédemment que lorsqu'un conducteur est suffisamment loin de la terre on peut lui associer une capacité intrinsèque qui ne dépend que des caractéristiques géométriques du conducteur et de la permittivité du milieu dans lequel il est plongé (ε0 pour le vide).

Le conducteur isolé
Pour simplifier les expressions on choisit arbitrairement que le potentiel sur la terre ou la masse distante est nul. On peut étendre cette situation aux régimes lentement variables dans la mesure ou le conducteur reste quasiment à chaque instant en équilibre électrique, dans la pratique c'est le cas tant que les dimensions de l'électrode restent nettement plus petites que les longueurs d'ondes obtenues dans le milieu extérieur et que le fil de liaison est suffisamment court et fin pour que la quantité de charges accumulées le long du fil soit négligeable devant celle accumulée sur la surface du conducteur.

Et son extension dans le cadre des circuits
Ordres de grandeur
Rappelons que les capacitances obtenues pour des conducteurs de taille centimétrique sont dans la gamme du picofarad à la limite du femtofarad et qu'ainsi les effets des self capacitances sont négligeables dans les circuits usuels. La situation devenant différente dans les cas où l'on considère à la fois des hautes tensions et des relativement hautes fréquences tout en restant dans le cadre quasi statique. Donnons deux exemples pour illustrer cela. Considérons un conducteur ayant une self capacitance de 1pF soumis dans un premier temps à une tension alternative de 100V et 50 Hz. La puissance réactive qui traverse ce circuit (énergie stockée/libérée par unité de temps) est donnée par :
![]()
On obtient avec les données précédentes une puissance réactive de 1,5 μW (microwatt) qui est bien entendu totalement négligeable par rapport aux autres puissances présentes dans les circuits usuels.
Considérons maintenant le même petit conducteur soumis cette fois à une tension alternative de 3kV et 300kHz, le lecteur n'aura aucun mal à se convaincre qu'une telle fréquence appliquée à un si petit conducteur ne rayonne qu'une énergie EM infime (il faut atteindre le GHz pour que l'énergie rayonnée devienne importante), la formule précédente nous donne cette fois une puissance réactive de 8,5 W !!!!
Le domaine hautes tensions hautes fréquences concerne donc
des tensions du type de celles rencontrées en électrostatique, voir plus faibles,
qui sont manipulables simplement avec les composants actuels (les tensions
présentes dans un moniteur cathodique d'ordinateur sont de l'ordre de 30kV) et
les fréquences bien que plus élevées que celles utilisées normalement pour la
distribution électrique, sont encore beaucoup trop basses pour générer un
rayonnement EM mesurable, elles sont régulièrement utilisées dans les
alimentations à découpage modernes. Ce domaine, totalement inaccessible du temps
de Maxwell, est maintenant à la portée des technologies courantes.
Le dipôle isolé
Comme dans le cas magnétique, la linéarité de l'équation de Poisson conduit à des expressions linéaires entre les charges présentes sur les conducteurs parfaits et les potentiels et inversement. Pour deux conducteurs parfaits isolés on peut donc écrire :
![]()
On peut démontrer que ce système n'est jamais dégénéré et donc que l'on peut exprimer aussi les charges en fonction des tensions sous la forme suivante :
![]()
La situation est finalement très similaire à celle du couplage magnétique, les signes moins provenant de l'inversion, on peut définir les self capacitances des conducteurs (généralisation de la notion de capacité intrinsèque en présence d'autres conducteurs) et des capacitances mutuelles, d'après le théorème de réciprocité nous avons C12 = C21 = CM , on peut aussi poser C11 = C1 et C22 = C2 pour simplifier les notations.
Influence partielle et totale
Faisons maintenant une petite parenthèse pour expliciter une difficulté spécifique aux couplages électriques. Considérer seulement deux conducteurs avec des charges qui ne soient pas simplement opposées nécessite de considérer forcément au moins un troisième objet distant qui porte l'excédent ou le déficit de charge. Une autre manière équivalente de poser le problème est de constater que pour pouvoir mesurer deux potentiels différents il faut avoir une référence de potentiel commune qui ne soit pas l'une des électrodes. En l'absence de se troisième objet distant, on ne peut considérer que le cas ou les charges mises en oeuvres sont opposées et ou la seule tension mesurable est celle existant entre les deux conducteurs. Dans un tel cas, qui correspond à une matrice de couplage quasiment dégénérée (dont le déterminant est quasi nul), la situation se ramène à : Q1= -Q2 = CV12 soit : Q=CV. Intuitivement on comprend bien que les deux charges étant seules, les lignes de champ qui quittent le premier conducteur atteignent toutes le deuxième, en conséquence les deux charges partagent l'intégralité du flux électrique il n'y a aucun flux de fuite et le couplage est total, on dit aussi que les charges sont en influence totale.



Influence totale
On peut obtenir une situation d'influence partielle plus générale que celle concernant le condensateur usuel en considérant une troisième électrode, la terre par exemple, qui porte la charge manquante et qui sert de référence de potentiel, mais qui soit suffisamment distante pour ne pas influencer la distribution des lignes de champs autour des deux conducteurs. Ainsi, tout comme nous avons pu considérer un monopole isolé en le considérant comme loin de la terre, on peut naturellement considérer un dipôle isolé loin de la terre. Insistons sur le fait que la terre, ou n'importe quelle électrode de grande taille suffisamment distante pour ne pas perturber sensiblement le champ proche entre les deux électrodes du dipôle, a un double rôle, celui de porter la charge différentielle du dipôle afin que le problème global soit électriquement neutre et surtout fournir une référence pour la mesure des potentiels des deux électrodes du dipôle. Il existera cette fois des lignes de champ qui quitteront l'une des électrodes sans rejoindre la seconde et inversement certaines lignes aboutiront sur cette électrode sans provenir de la première, ce sont les flux associés à ces lignes qui joueront le rôle de flux de fuites dans le cas du couplage électrique partiel. Nous demandons au lecteur d'admettre que comme pour une électrode isolée (loin de la terre) la configuration des lignes de champ est indépendante de cette troisième électrode qui joue ainsi un rôle virtuel si elle est suffisamment distante.
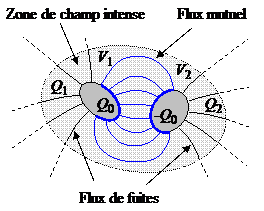


Influence partielle et rôle virtuel de la référence de potentiel
Cette approche que certains trouveront, comme celle de conducteur isolé surprenante, nous permet d'introduire très simplement deux circuits couplés en reliant via des branches séparées chacun des conducteurs à la terre distante. Pour convaincre les récalcitrants qui spontanément aborderaient ce problème en mettant sur un même pied d'égalité les trois électrodes (c'est à dire en considérant une matrice 3x3 pour le couplage), nous montrerons dans le paragraphe suivant que l'étude d'un quadripôle électrique, situation encore plus générale, se ramène dans le cadre des circuits, moyennant certaines restrictions que nous préciserons, à celle des deux conducteurs loin de la terre que nous abordons maintenant. La justification de cette approche sera donc établie totalement à posteriori.

Extension au cadre des circuits couplés
Nous avons en régime variable i1 = dq1/dt = q1'= C1v1'-CMv2' et i2 = -dq2/dt = q2'= -CMv1'+C2v2' on obtient finalement :
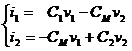 |
Soit sous forme matricielle compacte : |
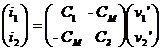 |
Notons que bien que le couplage électrique prenne une forme matricielle similaire, les rôles des tensions et courants sont inversés. Le déterminant du système est : Det = C1C2 - CM², il ne s'annule jamais si : CM² < C1C2
Le coefficient de couplage électrique se définit simplement par :
![]()
Il apparaît comme le rapport de la capacitance mutuelle à la moyenne géométrique des self capacitances. Comme le flux électrique mutuel ne peut pas être plus grand que le flux qui atteint chacune des électrodes, le coefficient de couplage est nécessairement plus petit que l'unité, le problème n'est jamais dégénéré.
Le quadripôle isolé
De la même manière nous allons considérer maintenant le cas d'un système de quatre conducteurs distants en équilibre quasi statique et suffisamment éloignés de la référence de potentiel.

Le quadripôle isolé en équilibre électrostatique
Une telle configuration est totalement décrite dans le cadre de l'électrostatique par une matrice 4x4, toutefois compte tenu du théorème de réciprocité la matrice est symétrique et implique n(n+1)/2 coefficients capacitifs différents soit 10 coefficients pour n=4 (on retrouve 3 coefficients pour n=3).
La généralisation au cadre dynamique non rayonnant est obtenue naturellement, elle est décrite dans le cas le plus général par la même matrice complémentée par les lois des noeuds mailles et dipôles (ou multi pôles externes). Il existe toutefois une famille de situations ou le problème se simplifie notablement qui correspondent aux cas ou les circuits externes se ramènent à seulement deux branches que l'on peut appeler en suivant nos amis anglo-saxons : "dispositifs à deux ports".
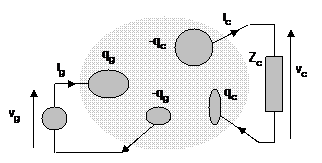
Dispositif quadripolaire à deux ports
Dans de tels dispositifs les quatre électrodes sont connectées deux à deux via deux branches extérieures seulement. Si on ne considère que des régimes oscillants, nécessaires pour que de l'énergie puisse être transmise à distance, les oscillations de charge sont nécessairement égales sur deux électrodes connectées au même circuit externe, les courants entrants et sortants étant égaux. Si de plus on ne s'intéresse qu'aux tensions entrantes et sortantes correspondantes de chaque côté, que nous appellerons respectivement générateur et charge, il ne reste plus comme variables significatives que deux charges, deux courants et deux tensions, soit la même situation que celle précédente du dipôle étendu au cadre des circuits via deux branches reliées à la masse distante. Pour l'obtenir nous avons du nous restreindre à une conditions particulière d'utilisation du quadripôle mais aussi à ne mesurer que des différences de tension particulières. Ainsi les tensions qui peuvent exister entre électrodes coté générateur et celles côté charges, et qui peuvent avoir cependant une grande importance pratique, ne sont pas prises en compte par ce modèle. La description précédente est cependant suffisante pour étudier les transfert d'énergie à distance.
Cette situation de quadripôle à deux ports est la plus générale que l'on puisse imaginer dans le domaine électrique pour obtenir deux circuits couplés par influence. Elle se ramène, comme dans le cas du couplage magnétique, à considérer deux dipôles oscillants couplés en champ proche. Lorsque l'on ne considère que les échanges d'énergie, la situation électrique se décrit aussi par une matrice de couplage 2x2 symétrique (à trois coefficients). Par contre, du à l'existence de monopoles que l'on peut isoler, la situation électrique est en général plus complexe que celle magnétique et implique pour sa totale détermination une matrice 4x4 symétrique (à 10 coefficients).
Les représentations
Bien que nous ayons vu que le cas du condensateur usuel soit un cas de couplage particulier (influence totale) qui corresponde à une matrice de couplage dégénérée (qui se ramène à un seul coefficient) et ne soit pas à priori adapté pour décrire des situations de couplage plus générales, le premier réflexe bien naturel est de transposer cette nouvelle situation en termes connus et bien maîtrisés.
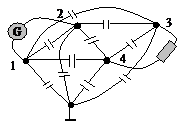

La représentation des 10 coefficients capacitifs en termes de condensateurs usuels
Les noeuds 1 à 4 concernent une répartition virtuelle de courants de déplacements au niveau de chaque électrode. Par exemple le noeud 1 explicite que le courant matériel provenant du générateur se transforme en quatre courants de déplacement, trois qui rejoignent les autres électrodes matérielles du circuit et le quatrième la terre (ou la masse) distante. Le cas du noeud associé à la terre est encore plus étonnant car il n'a aucune correspondance matérielle. On voit bien sur cet exemple à quel point vouloir absolument décrire une situation en termes connus peut conduire à des représentations lourdes où certaines branches sont totalement virtuelles et ne correspondent à aucun courant matériel mesurable.
Inversement dans le cas extrême opposé où l'on ne s'intéresse qu'aux échanges d'énergie on peut ne faire figurer, comme nous l'avons fait jusqu'a présent, que les éléments et courants matériels mais rendre la description plus symbolique en ne faisant figurer que les éléments clés, la transposition directe du cas magnétique devient ainsi :

La transposition de la représentation symbolique au cas du couplage électrique
Si l'on cherche à représenter les choses en terme de partie commune, les représentations qui conduisent aux relations les plus simples sont cette fois des représentation en "π", cela découle du fait que les rôles des courants et tensions sont inversés par rapport au couplage magnétique, les noeuds sont ainsi remplacés par des mailles et inversement, ceci est exprimé mathématiquement sous forme du théorème de dualité. Pratiquement cela nous conduit à envisager la représentation suivante :
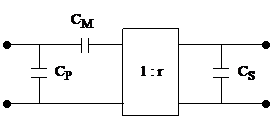
Représentation duale du couplage magnétique pour le cas électrique
Toutefois comme nous l'avons vu la symétrie entre les deux cas de couplage n'est pas totale, il n'y a pas dans le cas électrique de rapport lié à un nombre de tours différents et on ne peut pas réaliser simplement de transformateur électrique à l'aide de simple agencement d'électrodes. Le cas électrique correspond donc à des enroulements couplés qui auraient des nombres de tours identiques et donc un rapport de transformation égal à l'unité. On peut mieux comprendre ce point en notant que dans le cas du couplage magnétique l'énergie électrique est transformée en énergie magnétique dans le premier enroulement puis après couplage l'opération contraire est effectuée, dans le cas du couplage électrique on ne passe pas par un intermédiaire qui permette de changer d'échelle. La transposition duale qui permettrait d'obtenir une dualité parfaite serait obtenue si on considérait deux circuits magnétiques couplés électriquement. Il en résulte un théorème spécifique aux couplages électriques entre circuits électriques qui affirme que les coefficients du modèle en "π" sont toujours positifs.
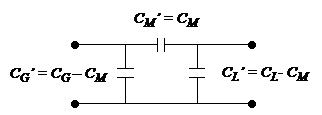


Représentation générale pour les échanges d'énergie du couplage électrique par le modèle en "π"
Bien entendu les modélisations précédentes ne tiennent dans le cas des quadripôles que pour l'étude des échanges d'énergie. Nous reviendrons sur ces problèmes de représentation dans la partie consacrée à l'étude détaillée de la technologie de couplage électrique qui combine l'usage de monopoles isolés avec celui d'influence partielle selon la configuration longitudinale suivante :
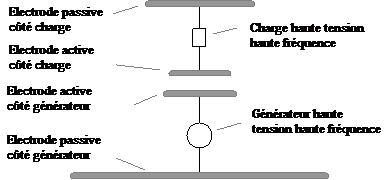


La configuration proposée dans les brevets récents pour le couplage électrique en champ proche
Développer davantage le formalisme et les concepts
Non merci, notions suivantes SVP